Flow around the cylinder 2D single level
Warning
WORK IN PROGRESS
Navigate: ← Test Case Channel 2D
Flow around the cylinder in a channel 2D
This example looks at the flow though a 2D channel with a cylinder placed into it and a mesh of multiple levels to better resolve the flow close to walls.
Problem description
The Poiseuille flow is the fully developed laminar flow between two parallel plates induced by a constant pressure drop in a channel of length L. We place a cylinder into that channel as a disturbance and look at the flow around this cylinder. In general, the flow can be induced by any of the following way:
- Defining pressure at inlet and outlet of the channel.
- Defining velocity at inlet and pressure at outlet of the channel.
- Using pressure gradient i.e. pressure drop/length as a external force.
Here, the flow is induced by pressure boundary conditions at inlet (west) and outlet (east) boundaries.
The pressure drop along the channel per unit length is where,
- - the maximum fluid velocity at the channel center axis,
- - the fluid density and
- - kinematic viscosity.
Note
In this testcase we compute the viscosity according to the Reynolds number and the speed of sound according to the Mach number.
The Reynolds number is defined as where, - the mean velocity. For the parabolic velocity profile, the mean velocity can be computed with .
Post-processing
Tracking relevant quantities gives us the following visualizations:
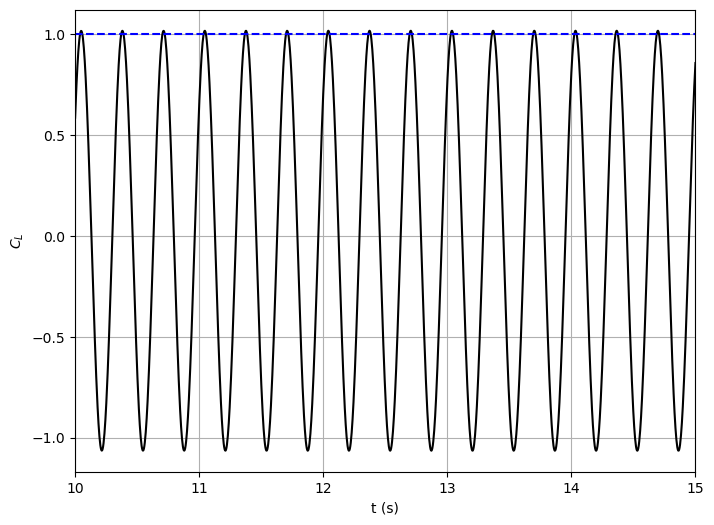
Lift coefficient of the cylinder over time:
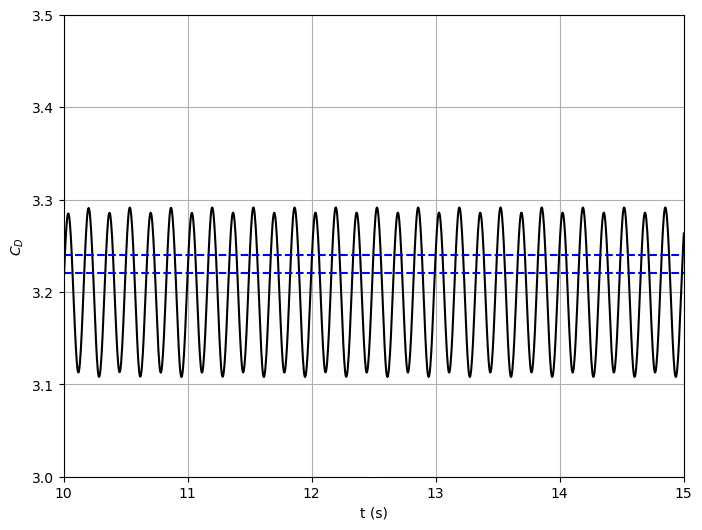
Drag coefficient of the cylinder over time:
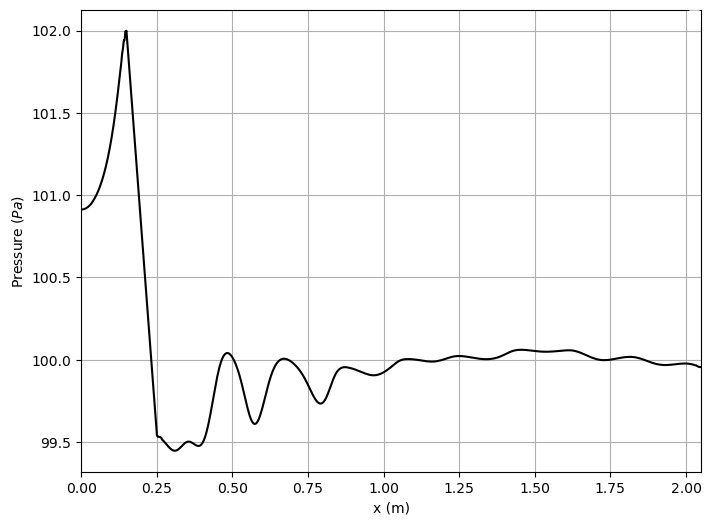
Pressure along the length of the channel:
Pressure coefficient over the cylinder surface:

Pressure difference between stagnation in front of cylinder
and back of the cylinder over time:

The X-velocity component along the length of the channel:

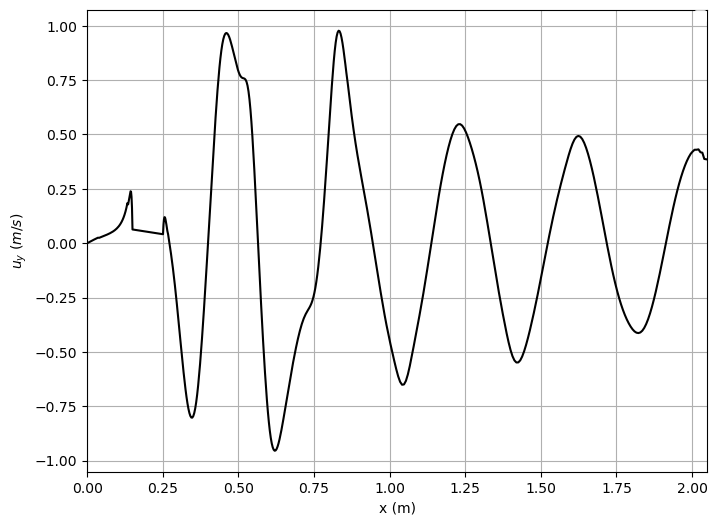
The Y-velocity component along the length of the channel:
A Fourier transform of the flow field:
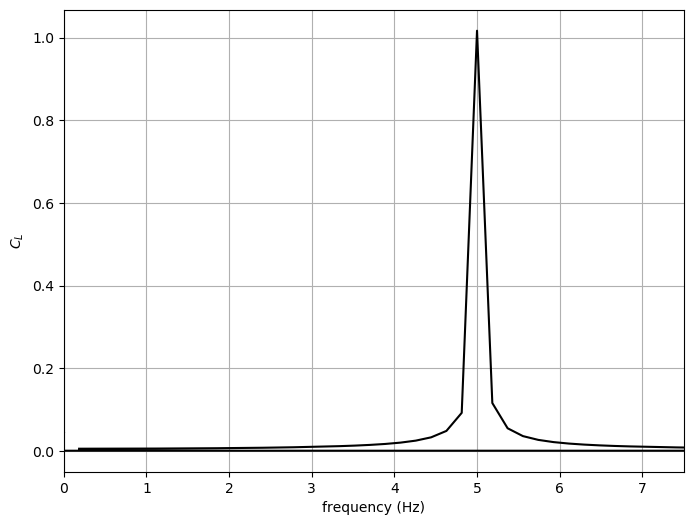
To create these plots, run python plot_track.py to create the plots. Before running the plot script, open 'plot_track.py' and update path to Gleaner script in 'glrPath'. Download Gleaner script using hg clone https://geb.inf.tu-dresden.de/hg/gleaner