Gaussian Pulse in Pressure in a Cube
Warning
WORK IN PROGRESS
Progress of this test case is tracked in the following ticket: Action #2206: Test case - Benchmark: Gaussian pulse
Gaussian Pulse in Pressure in a Cube
In this example, we will simulate a Gaussian pulse in pressure in a simple pre-defined cube with periodic boundaries and user-defined initial condition. The gaussian pulse can be also used via a lua function, c. f. * lua-function of gaussian pulse For this simple geometry, we even do not need Seeder.
The objectives of this example is to introduce how to: * Use a pre-defined geometry instead of creating a mesh with Seeder. * Simulate the Gaussian pulse in the cube using Musubi. * Create 2D plots using the Gleaner tool. Gleaner is a Python tool that extracts data from Musubi ASCII output and uses the plotting library Matplotlib in Python to create a plot. * Validate the numerical results by comparing them against the analytic solution. The latter one is calculated using NumPy, a mathematic extension for Python. * Compare the simulation results (L4) to previously generated data obtained with higher resolution (reference folder, L5 & L6) to experience the influence of the resolution.
ToDo
This file has to be filled with content like: * Problem description * Formulas * Results * Comparison for different resolutions * How to run the simulation
Here are the results from the simulation.
Pressure across the length of the channel for different resolutions at the
beginning (initial condition):
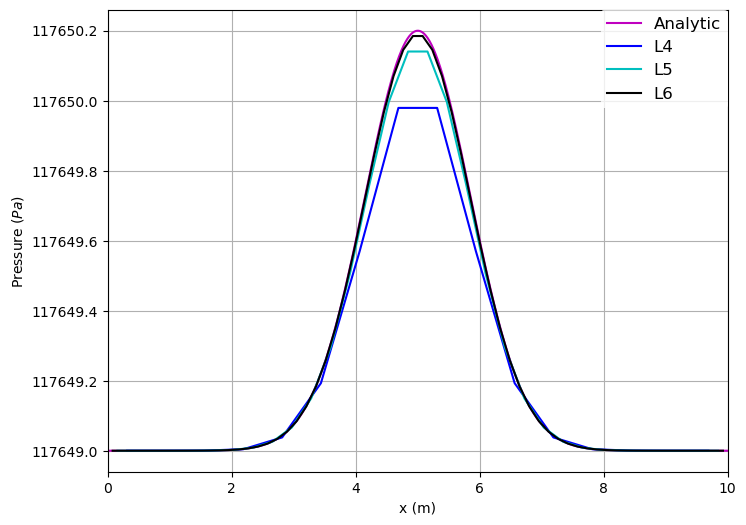 The higher the level -- and with that the resolution -- the better the solution
compared to the analytical one.
The higher the level -- and with that the resolution -- the better the solution
compared to the analytical one.
Pressure across the length of the channel for different resolutions at the end:
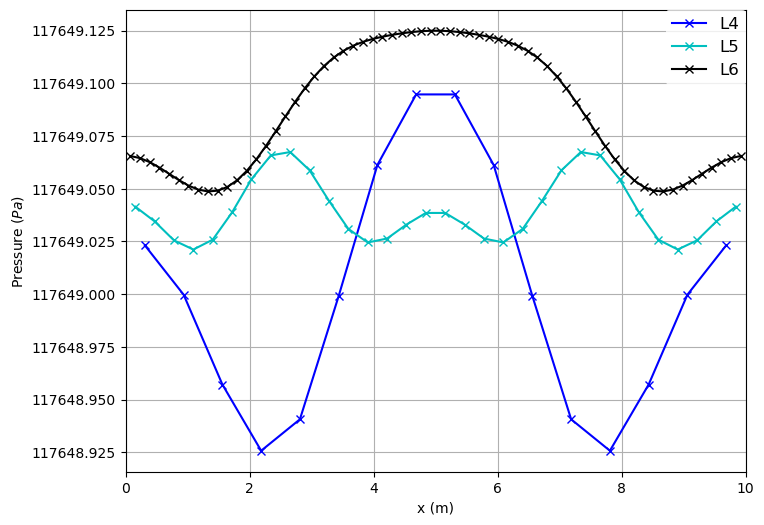 It can be seen that the resolution has a great impact on the results.
It can be seen that the resolution has a great impact on the results.
To create these plots, run python plot_track.py to create the plots. Before running the plot script, open 'plot_track.py' and update path to Gleaner script in 'glrPath'. Download Gleaner script using hg clone https://geb.sts.nt.uni-siegen.de/hg/gleaner